4.Выборка
4.2 Вероятностная выборка
Вероятностные выборки - Требуют полного знания генеральной совокупности
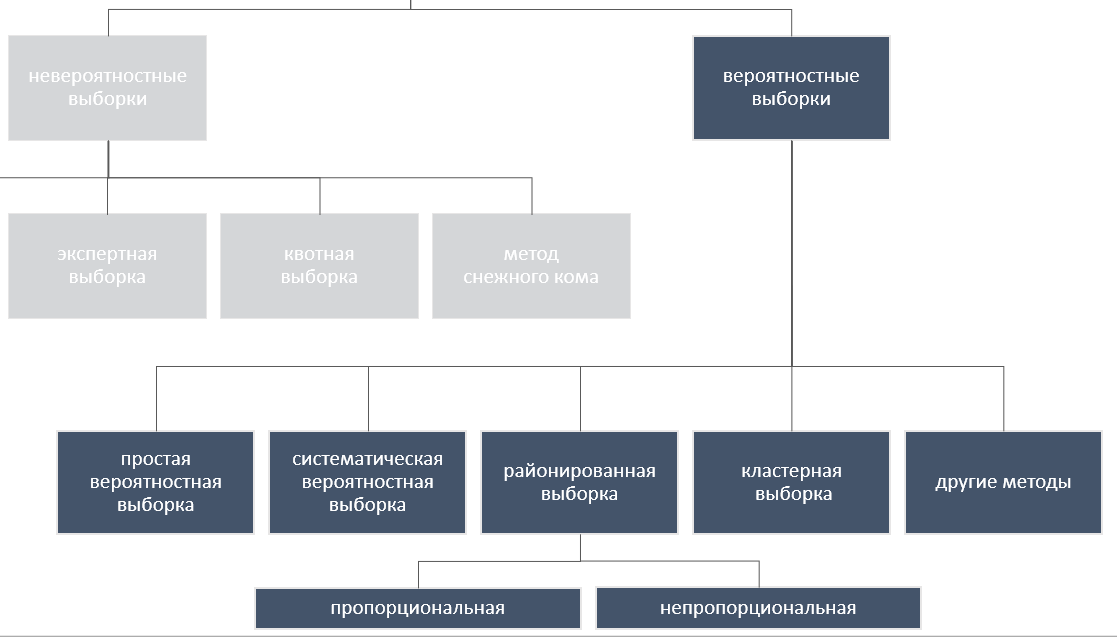
Простая и систематическая вероятностные выборки
Простая и систематическая вероятностные выборки - Требуют полного знания генеральной совокупности
Простая вероятностная выборка
Каждый элемент выборки выбирается случайно и независимо от любого другого элемента. Это означает, что:
- Каждый элемент генеральной совокупности имеет известную и равную вероятность быть выбранным.
- Каждая возможная выборка заданного размера (n) имеет известную вероятность быть на самом деле выбранной.
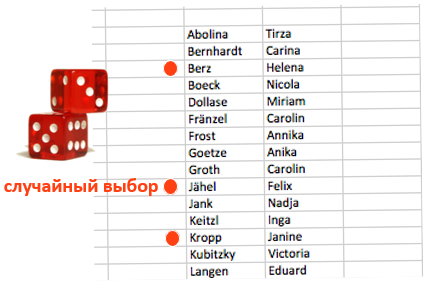
Систематическая вероятностная выборка
- Первый элемент выборки выбирается случайно, затем, с постоянным шагом отбирается каждый i-ый элемент.
- Шаг отбора i определяется путем деления размера генеральной совокупности N на размер выборки n, то есть i = N/n

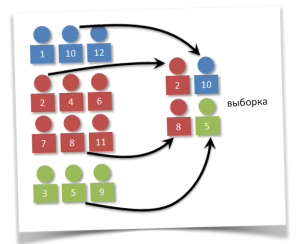
Районированная выборка
Районированная выборка - Требует полного знания генеральной совокупности
Районированная выборка также называется стратифицированной выборкой.
Генеральная совокупность разбивается на однородные непересекающиеся группы (страты), затем из каждой страты производится отбор случайным образом.
Метод особенно хорош для
- выделения определенной подгруппы внутри генеральной совокупности,
- наблюдения существующих взаимосвязей между двумя и более подгруппами,
- репрезентативной выборки даже самых маленьких и труднодоступных подгрупп генеральной совокупности,
- более высокая статистическая точность
Пропорциональная
| Страта |
A |
B |
C |
|
Размер ген. совокупности |
100 |
200 |
300 |
|
Доля выборки |
1/2 |
1/2 |
1/2 |
|
Размер выборки |
50 |
100 |
150 |
Непропорциональная
| Страта |
A |
B |
C |
|
Размер ген. совокупности |
100 |
200 |
300 |
|
Доля выборки |
1/5 |
1/2 |
1/3 |
|
Размер выборки |
20 |
100 |
100 |
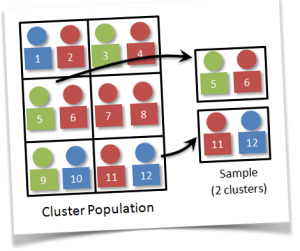
Кластерная выборка
Кластерная выборка - Требует полного знания генеральной совокупности
Кластерная выборка также называется серийной или гнездовой выборкой.
Генеральная совокупность сначала делится на взаимоисключающие и взаимодополняющие подгруппы (кластеры). Затем с помощью вероятностного метода выборки, формируется случайная выборка кластеров.
Метод особенно хорош для
- покрытия больших географический районов,
- снижения стоимости исследования,
- когда построение полного списка элементов генеральной совокупности затруднительно,
- когда генеральная совокупность сосредоточена в естественных кластерах (например, кварталы, города, школы, больницы, коробки и т.д.)